RSI indicator finally explained

truth, the whole truth and nothing but the truth


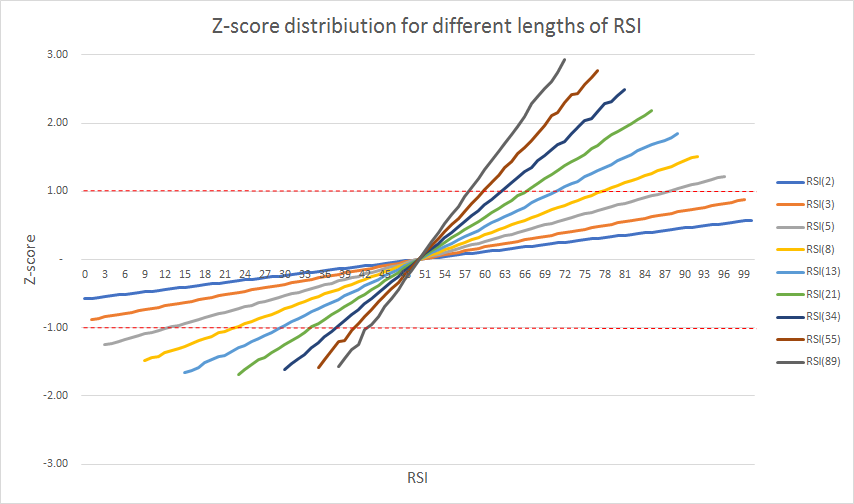
RSI demystified: part 1 part 2 part 3

In the previous articles we investigated the properties of Relative Strength Index. What we know so far, is that when RSI crosses the 50-point line it means that price crosses the exponential moving average of corresponding length (2*period-1). We also discovered that overbought (70-points) and oversold (30-points) levels are associated to volatility band that can be drawn around moving average. 70-point line for RSI(14) equals upper (+1) volatility band from moving average, and 30-point line equals lower (-1) volatility band from moving average. Right now, it’s time to check the behavior of other period lengths used for RSI calculation. We will still use the same logic for constructing volatility band, so it is recommended to read previous articles before continuing.

Any numbers are equally good, but we will use numbers from Fibonacci sequence (geometric growth) instead of any fixed interval (linear growth). We will start with RSI(2), RSI(3) … and finish with RSI(89). And, yes – I know – no one uses RSI(89)… Well, we’re about to find out why.

multirsi
Close

There is one thing that is consistent with previous discoveries: No matter the period length for RSI, the 50-point line is still an exponential moving average of the corresponding length. But when we compare how zscore translates into levels that RSI indicator reaches, then we see, that the +1 and -1 zscore is never reached by RSI(2) and RSI(3), and is really quickly reached by RSI(55) or RSI(89). So even when RSI(2) drops to 1 point or go as high as 99 points the zscore is still way above -1 or below 1. On the other hand, RSI(89) moving to 58-points already translated into +1 zscore and dropping to 42-points translates to -1 zscore. This means that any attempt to average or compare RSIs of different lengths in order to get the full picture of market situation is a wasted effort.

But this in not the only problem we have with the behavior of RSI of different lengths. Even from the above chart we see that RSI(2) can take pretty much any number between 0 and 100, and RSI(89) will barely reach 70-points and in the last 10 years (S&P500 futures) did not drop below 37-points. The asymmetry in positive and negative extremes are caused by the current bull market, so the next pictures will be built using almost 20 years of data for S&P500 index.

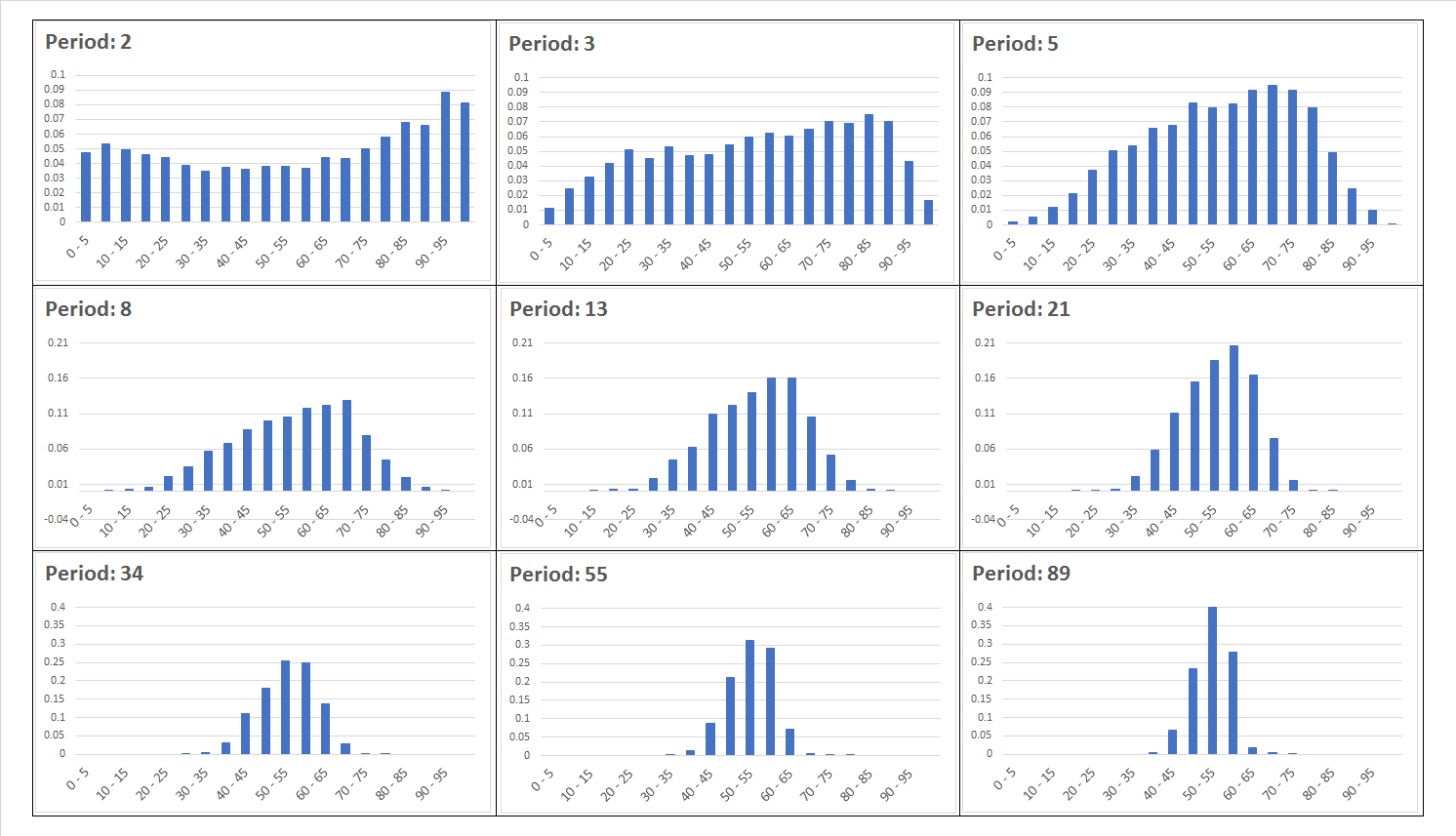
multirsi
Close

The above picture shows the distributions of RSI readings depending on the period length. Starting from the shortest period we get a bimodal distribiution (RSI(2) will most of the time be in a 5-10 or 90-95 point bin) that through almost uniform distribiution of RSI(3) transforms into platykurtic distribiution (RSI(5) and RSI(8)). After that we finally go to something that we know and are used to: normal distribiution aka “the bell curve”. This happens when RSI length is set to 13 or 21. Once we move into “long term territory” (34,55,89) the density function gets more and more leptokurtic.

So, this is another view of the same problem with RSI. The trader, without dropping its habits, just can’t get a good deal of valuable information from short or long term period RSIs, because only mid-term lengths (the one and only RSI(14)) show the picture of the market through the lens that we are used to: the bell curve.

The mistakes that come from using the normal distribution with financial data is a longer and more complex story, so for now let’s just stick to the main subject – RSI indicator.

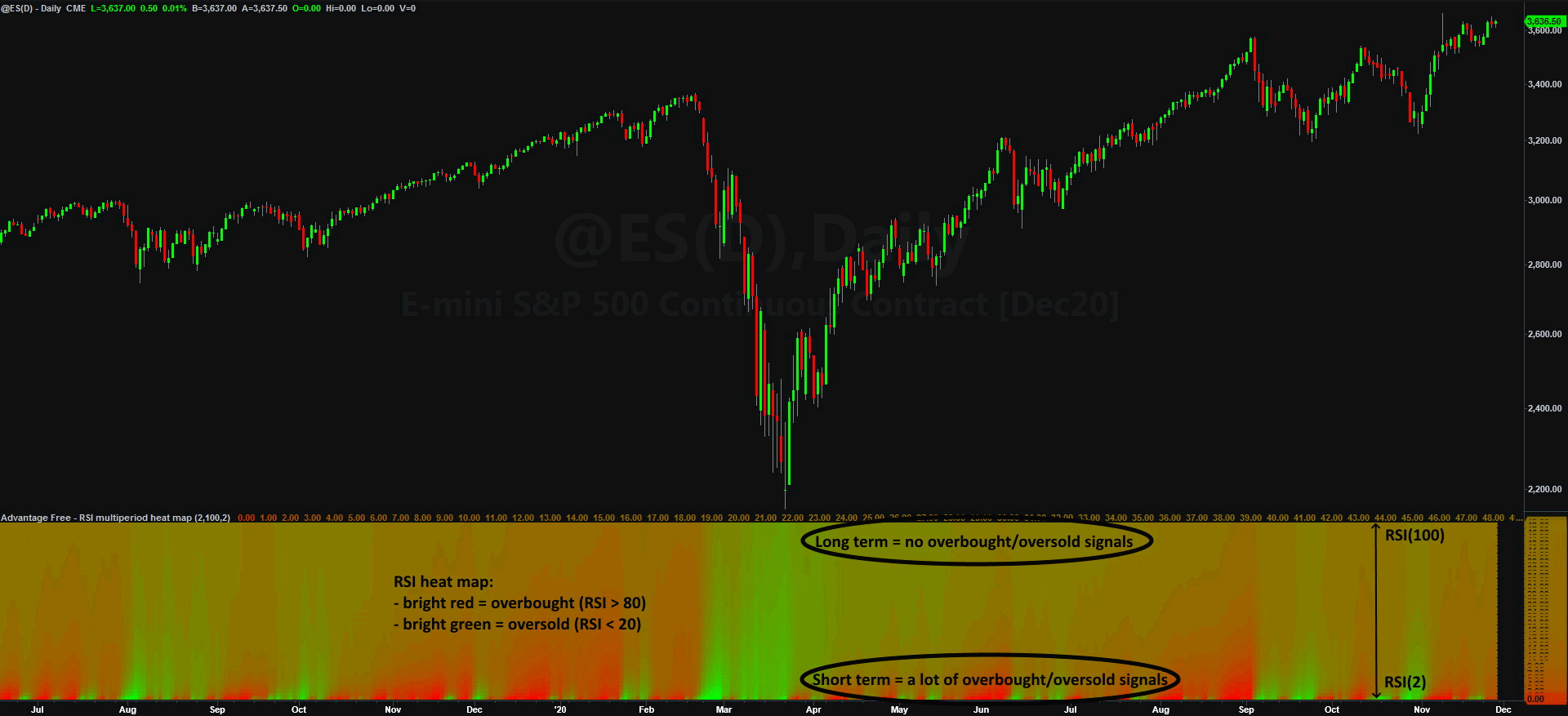
We just discussed that RSI indicator is badly calibrated. It shows one kind of properties for short term settings, other properties for medium term settings and totally different properties for long term settings. The best visualization we get by looking at the heat map, where we plot 50 different RSI lengths at once. The idea is simple – put more and more red when RSI is high (>80), put more and more green when RSI is low(<20).

rsiheatmap
Close

The first row from the bottom is RSI(2) and the top one is RSI(100). The information we get from this chart is not a surprise. The bottom rows change colors from bright red (overbought) to bright green (oversold) really frequently, which is consistent with the previous chart, where RSI(2) has a bimodal distribution. And the top rows, where long period RSIs are plotted, barely get affected by price movements. The only things that change are the pale shades of red or green. And of course, this is also expected, because long term RSIs rarely brake from 40- to 60-point range.

Well, we pretty much deciphered RSI. We know that:

• When RSI(period) crosses the 50-point line, price crosses exponential moving average of a corresponding length (2*period – 1)
• For RSI(14) 70-point line equals +1 volatility (scaled) from ExpMov(27) and 30-point line equals -1 volatility (scaled) from ExpMov(27)
• RSI is a zscore (distance) of price from exponential moving average, for which the scaling factor (square root of period) is not working properly
• Wrong calibration of scaling factor makes impossible to average or compare RSIs of different lengths
• If you want to stay with RSI(14) only, you’re fine. If not – you either need a solution, or are forced to work with constrains that cannot be overcome.

From now on, if you encounter RSI indicator ever again you will know exactly what you see. You will be immune to supposedly magical properties of RSI trading systems, or secret patterns that few know. Hopefully it will make you a more aware trader.

RSI demystified: part 1 part 2 part 3




All information and findings provided by AdvantageTrading.Net are intended solely for educational purposes related to exchange trading and by no means serve as investment or trading advice. In case there are particular financial instruments, trading strategies, Easylanguage formulas, tradestation indicators, money management and risk management techniques, underlying assets or derivatives mentioned on www. http:// advantagetrading.net /, training courses, educational materials, downloads, presentations, videos, webinars or online courses, it is always and solely for educational purposes. AdvantageTrading.Net and authors of educational materials, Tradestation strategies, indicators, articles, documents and videos, or any lecturers are in no case responsible for particular trading decisions of individual traders, users of our products or services or participants of our training courses, which are presented on this website. The systems and the analysis techniques contained objective rules and values to enter and exit the market. No customized or other trading advice or recommendations are made by these products and values.
Commodity Futures Trading Commission Futures and Options trading has large potential rewards, but also large potential risk. You must be aware of the risks and be willing to accept them in order to invest in the futures and options markets. Don't trade with money you can't afford to lose. This is neither a solicitation nor an offer to Buy/Sell futures or options. No representation is being made that any account will or is likely to achieve profits or losses similar to those discussed in this report, or on our web site. The past performance of any trading system or methodology is not necessarily indicative of future results.
HYPOTHETICAL PERFORMANCE RESULTS HAVE MANY INHERENT LIMITATIONS, SOME OF WHICH ARE DESCRIBED BELOW. NO REPRESENTATION IS BEING MADE THAT ANY ACCOUNT WILL OR IS LIKELY TO ACHIEVE PROFITS OR LOSSES SIMILAR TO THOSE SHOWN. IN FACT, THERE ARE FREQUENTLY SHARP DIFFERENCES BETWEEN HYPOTHETICAL PERFORMANCE RESULTS AND THE ACTUAL RESULTS SUBSEQUENTLY ACHIEVED BY ANY PARTICULAR TRADING PROGRAM.
ONE OF THE LIMITATIONS OF HYPOTHETICAL PERFORMANCE RESULTS IS THAT THEY ARE GENERALLY PREPARED WITH THE BENEFIT OF HINDSIGHT. IN ADDITION, HYPOTHETICAL TRADING DOES NOT INVOLVE FINANCIAL RISK, AND NO HYPOTHETICAL TRADING RECORD CAN COMPLETELY ACCOUNT FOR THE IMPACT OF FINANCIAL RISK IN ACTUAL TRADING. FOR EXAMPLE, THE ABILITY TO WITHSTAND LOSSES OR TO ADHERE TO A PARTICULAR TRADING PROGRAM IN SPITE OF TRADING LOSSES ARE MATERIAL POINTS WHICH CAN ALSO ADVERSELY AFFECT ACTUAL TRADING RESULTS. THERE ARE NUMEROUS OTHER FACTORS RELATED TO THE MARKETS IN GENERAL OR TO THE IMPLEMENTATION OF ANY SPECIFIC TRADING PROGRAM WHICH CANNOT BE FULLY ACCOUNTED FOR IN THE PREPARATION OF HYPOTHETICAL PERFORMANCE RESULTS AND ALL OF WHICH CAN ADVERSELY AFFECT ACTUAL TRADING RESULTS.
Neither TradeStation Technologies nor any of its affiliates has reviewed, certified, endorsed, approved, disapproved or recommended, and neither does or will review, certify, endorse, approve, disapprove or recommend, any trading software tool that is designed to be compatible with the TradeStation Open Platform.
REFUND/EXCHANGE POLICY: You understand that you are purchasing downloadable software that is impossible to return. We do not offer refunds for that reason however, if you are dissatisfied we will offer an exchange of equal amount of your choice from our website (depending on Availability). All sales, any fees are non-refundable regardless of performance.